Torben Mogensen
email: torbenm@diku.dk
March 28, 2006
Most RPGs (role-playing games) use some sort of randomizer when resolving actions. Most often dice are used for this, but a few games use cards, rock-paper-scissors or other means of randomization.
There are dozens of different ways dice have been used in RPGs, and we are likely to see many more in the future. This is not an evolution from bad methods to better methods -- there is no such thing as a perfect dice-roll system suitable for all games (though there are methods that are suitable for none). But how will a designer be able to decide which of the existing dice-roll method is best suited for his game, or when to invent his own?
There is no recipe for doing this -- it is in many ways an art. But like any art, there is an element of craft involved. This paper will attempt to provide some tools and observations that, hopefully, will give the reader some tools for the craftmanship involved in the art of choosing or designing dice-roll mechanisms for RPGs.
Ever since Dungeons & Dragons was published in 1974, randomization has, with a few exceptions, been a part of role-playing games. Randomization has been used for creating characters, determining if actions are successful, determining the amount of damage dealt by a weapon, determining encounters (“wandering monsters”, etc.) and so on. We will look mainly at randomizers in action resolution -- the act of determining how successful an attempted action is. The reason for this is that this is in many ways the most critical part of an RPG and the part that is hardest to get right.
Mostly, dice have been used as randomizers, and D&D was indeed known for introducing non-cubic dice into modern games, but a few games (such as Castle Falkenstein and the Saga system) use cards as randomizers and some “diceless” games, like Amber, use no randomizers at all, apart from the inherent unpredictabiliy of human behaviour. We will focus on dice in this article, but briefly touch on other randomizers.
We will start by discussing some aspects of action resolution that it might be helpful to analyse when choosing a dice-roll mechanism, then a short introduction to probability theory followed by an analysis of some existing and new dice-roll mechanisms using the above. I will not follow a fixed structure when analysing the different systems, just babble a bit about what I find interesting, in the hope that this will spark some thoughts in the reader.
When a character attempts to perform a certain action during a game, there are several factors that can affect the outcome. We will classify these as ability, difficulty, circumstance and unpredictability.
Different resolution systems will take the above factors into account. Additionally, we below look at some other properties that action resolution systems might have and which a designer should think about, even if only to conclude that they are irrelevant for his particular game. Later, we shall look at various examples of resolution mechanisms and analyse them with respect to these properties.
So, is the best action resolution mechanism the one that models these aspects most realistically or in most detail? Not necessarily. First of all, more realism will usually also mean higher complexity, which makes your game more difficult to learn and play, and more detail will typically mean more categories (of skills, tasks, etc.) and larger numbers (to more finely distinguish between degrees of ability, success, etc.), which will require larger character sheets and more calculation. Nor is utmost simplicity necessarily the best way to go -- the result may be too inflexible and simplistic for proper use.
So what is the best compromise between simplicity and realism/detail? There is no single answer to that, it depends on the type of game you want to make. For a game (like Toon) that is designed to emulate the silliness of 1930's cartoons, the fifty-fifty rule (regardless of ability, difficulty and circumstance, there is 50% chance that you will succeed in what you do) is fine, but for a game about WW2 paratroopers, you would want somewhat more detail. Nor does detail and realism have to be consistent in a single game -- if the game wants to recreate the mood in The Three Musketeers, it had better have detailed rules for duels and seduction, but academic knowledge can be treated simplisticly, if at all. On the other hand, if the game is about finding lost treasure in ruins of ancient civilizations, detailed representation of historic and linguistic knowledge can be relevant, but seduction ability need not even be explicitly represented.
In short, you should not decide on an action resolution mechanism before you have decided what the game is about and which mood you want to impart.
In some games, ability and difficulty (including aspects of circumstance and predictability) are combined into a single number that is then randomized. In other games, ability and difficulty are separately randomized and the results are then compared, and you can even have cases where ability and difficulty affects randomization in quite different ways. Similar issues are whether active or reactive actions (e.g., attack versus defense) are treated the same or differently, whether opposed and unopposed actions are distinguished and how multiple simultaneous actions or sequences of actions that are chained into complex maneuvers are handled.
In the simplest case, all a resolution system needs to determine is “did I succeed?”, i.e., yes or no. Other systems operate with degrees of success or failure. These can be numerical indications of the quiality of the result or there might be just a few different verbal characterisations such as “fumble”, “failure”, “success” and “critical success”. Systems with numerical indications usually use the result of the dice roll more or less directly as degree of success/failure, while systems with verbal characterisations often use a separate mechanism to identify extreme results.
Some games, in particular superhero or SF games, operate with characters or character-like objects at scales far removed from humans in terms of skill, size or power. These games need a resolution mechanism that can work at vastly different scales and, preferably, also handle interactions across limited differences in scale (large differences in scale will usually make interactions impossible or one-sided). Some mechanisms handle scale very well, while others simply break down or require kludges to work.
Let us say we set a master up against a novice. Should the novice have any chance at all, however remote, of beating the master? In other words, shall an unskilled character have a small chance of succeeding at an extremely difficult task and shall a master have a small chance of failing at a routine task? Some games allow one or both of these to happen, while others implicitly or explicity don't.
Similarly, some tasks (like playing poker) are inherently more random than others (like playing chess), but few game systems distingush.
On a related note, the amount of random variability (spread) may be different for highly skilled persons and rank amateurs. In the “real world”, you would expect highly skilled persons to be more consistent (and, hence, less random) than unskilled dabblers, but, as we shall see, this is not true in all systems.
A GM might not always want to reveal the exact level of ability of an opponent to the players until they have seen him in action several times. Similarly, the difficulty of a task may not be evident to a player before it has been attempted a few times, and the GM may not even want to inform the players of whether they are successful or not at the task they attempt.
In all cases, the GM can decide to roll all dice and tell the players only as much as he wants them to know. But players often like to roll for their own characters, so you might want a system where the GM can keep, e.g., the difficulty level secret so the players are unsure if they succeed or fail or by how much they do so, even if they can see the numbers on their own dice rolls.
Many games makes it harder to improve one's ability the higher it already is. This is most often done through increasing cost in experience points of increasing skill or level, but it may also be done through dice: A player “pays” (either by using the skill or by spending a fixed amount of experience points) for a chance to increase a skill. Dice are rolled, and if the roll is higher than the current ability, it increases. Such mechanisms are used both in Avalon Hill's RuneQuest and in Columbia Games' HârnMaster.
Alternatively, you can have linear cost of increasing ability, but reduce the effectivenes of higher skills through the way abilities are used in the randomization process, i.e, by letting the dice-roll mechanism itself provide diminishing returns.
In order to fully analyse a dice-roll mechanism, we need to have a handle on the probability of the possible outcomes, at least to the extent that we can say which of two outcomes is most likely and if a potential outcome is extremely unlikely. This section will introduce the basic rules of probability theory as these relate to dice-rolling, and describe how you can calculate probabilities for simple systems. The more complex systems can be difficult to analyse by hand, so we might have to rely on computers for calculations, so we will briefly talk about this too.
Probabilities usually relate to events: What is the chance that a particular event will happen in a particular situation? Probabilities are numbers between 0 and 1, with 0 meaning that the event can never happen and 1 meaning it is certain to happen. Numbers between these mean that it is possible, but not certain for the event to happen, and larger numbers mean greater likelihood of it happening. For example, a probability of 1 2 means that the likelihood of an event happening is the same as the likelihood of it not happening. This brings us to the basic rules of probabilities:
Events are independent if the outcome of one event does not influence the outcome of the other. For example, when you roll a die twice, the two outcomes are independent (the die doesn't remember the previous roll). On the other hand, the events “the die landed with an odd number facing up” and “the die landed with a number in the upper half facing up” are not independent, as knowing one of these will help you predict the other more accurately. Taking any one of these events alone (on a normal d6), will give you a probability of 1 2 of it happening, but if you know that the result is odd, there is only 1 3 chance of it being in the upper half, as only one of 4, 5 and 6 is odd.
In the above, we have used an as yet unstated rule of dice: If a die is fair, all sides have the same probability of ending on top. In games, we usually deal with fair dice (all other considered cheating), so we will, unless otherwise stated, assume this to be the case. So, if there are n sides to the die, each has a probability of 1 n of being on top after the roll. The number on the top face or vertex is usually taken as the result of the roll (though some d4s read their result at the bottom edges). Most dice have results from 1 to n, where n is the number of sides of the die, but some ten-sided dice go from 0 to 9 and some have numbers 00, 10, 20, . . . , 90. We will use the term dn about an n-sided die with numbers 1 to n with equal probability and when we want to refer to other types, we will describe these explicitly.
If we have an event E , we use p(E ) to denote the probability of this event. So, the rules of negation and coincidence can be restated as
| p(not E) | = | 1 − p(E) |
| p(E1 and E2) | = | p(E1) × p(E2) |
We can use the rules of negation and coincidence to find probabilities of rolls that combine several dice. For example, if you roll two dice, the chance of both being ones (i.e., rolling “snake eyes”) is 1/36, as each die has probability 1/6 of being a one and 1/6 × 1/6 = 1/36 . The probability of not rolling snake eyes is 1 − 1/36 = 35/36 . But what about the probability of rolling two dice such that at least one of them is a one? It turns out that we can use the rules of negation and coincidence for this too: The chance of getting at least one die land on one is 1 minus the chance that neither land on ones, and the chance of getting no ones is the chance that the first is not a one times the chance that the other is not a one. So we get 1 − 5/6 × 5/6 = 11/36 . We can state the rule as
| p(E1 or E2) | = 1 − p(not E1) × p(not E2) |
| = 1 − (1 − p(E1)) × (1 − p(E2)) | |
| = p(E1) + p(E2) − p(E1) × p(E2) |
For another example, what is the chance of rolling a total of 6 on two d6? We can see that we can get 6 as 1 + 5, 2 + 4, 3 + 3, 4 + 2 and 5 + 1, so a total of 5 of the possible 36 outcomes yield a sum of 6, so the probability is 5/36 . Note that we need to count 1 + 5 and 5 + 1 separately, as there are two ways of rolling a 1 and a 5 on two d6, unlike the single way of getting two 3s.
In general, when you combine several dice, you count the number of ways you can get a particular outcome and divide by the total number of rolls to find the probability of that outcome. When you have two d6, this isn't difficult to do, but if you have, say, five d10, it is unrealistic to enumerate all outcomes and count those you want. In these cases, you either use a computer to enumerate all possible rolls and count those you want, or you find a way of counting that doesn't require explicit enumeration of all possibilities, usually by exploiting the structure of the roll.
For simple cases, such as the chance of rolling S or more on x dn, some people have derived formulae that don't require enumeration. These, however, are often cumbersome (and error-prone) to calculate by hand, so you might as well use a computer. For finding the chance of rolling S or more on x dn, we can write the following program (in sort-of BASIC, though it will be similar in other languages):
count = 0
for i1 = 1 to n
for i2 = 1 to n
...
for ix = 1 to n
if i1+i2+...+ix >= S then count = count + 1
next ix
...
next i2
next i1
print count/(n^x)
Each loop runs through all values of one die, so in the body of the innermost loop, you get all combinations of all dice. You then count those combinations that fulfill the criterion you are looking for. In the end, you divide this count by the total number of combinations (which in this case is nx). Such programs are not difficult to write, though it gets a bit tedious if the number of dice can change, as you need to modify the program every time (or use more complex programming techniques, such as recursive procedure calls or stacks). To simplify this task, I have developed a programming language called Roll specifically for calculating dice probabilities. In Roll, you can write the above as
sum x # d n
and you will get the probabilities of the result being equal to each possible value, as well as the probability of the result being less than each possible value. To find the chance of the result being greater than or equal to a value, you can use the negation rule: p( ≥ S) = 1 − p(< S). Alternatively, you can write:
count >=S (sum x # d n)
which counts only the results that are at least S. You can find Roll, including instructions an examples, at [http://www.diku.dk/~torbenm/Dice.zip].
If you can assign a value to each outcome, you can calculate an average (or mean) value as the sum of the probability of each outcome multiplied by its value. More precisely, if the possible outcomes are E1 , . . . , En and the value of outcome Ei is V(Ei), then the average of the outcomes is p(E1) × V (E1 ) + · · · + p(En) × V (En). For a single d6, the average is, hence, 1 × 1/6 + · · · + 6 × 1/6 = 21/6 = 3.5. In general, a dn has average (n + 1)/2 . If you add several dice, you also add their averages, so, for example, the average of x dn is x × ( (n + 1) / 2 ) . The variance of a number or outcomes with values is the sum of the squares of the distances of the values from the mean, i.e.,
where M is the mean value, as calculated above. This can be rewritten to
I.e., the average of the squares minus the square of the average. For a single dn, this adds up to (n2 − 1)/12 . For example, the variance of a d6 is 35/12 . When you add two dice, you also add their variances (like you do with averages), so the variance of the sum of five d6 is 5 × 35/12 = 175/12 , and so on.
It is, however, more common to talk about the spread (or standard deviation) of the outcomes. The spread is simply the square root of the variance. Examples: The spread of a d6 is SQRT( 35/12 ) = 1.7078 and the spread of 5d6 is SQRT( 175/12 ) = 3.8188.
The spread is a measure of how far away from the average value you can expect a random value to be. So if the spread is small, most values cluster closely around the average, but if the spread is large, you will often see values far away from the average. If two rolls have spreads s1 and s2 , then their sum has spread SQRT(s12 + s22) (as the spread is the square root of the variance).
Note that the spread is not the average distance from the mean value. The latter is called the mean deviation, and (while intuitively more natural) isn't used as much as the standard deviation, mostly because it isn't as easy to work with. The mean deviation is defined as
where |x| is the absolute value of x. For a single dn, the mean deviation is n/4. It gets more complicated when you add several dice, as (unlike for standard deviation), you can't compute the mean deviation of the combined roll from the mean deviations of the individual rolls. For example, d5 and 2d4 both have mean deviation 5 4 , but 2d5 has mean deviation 8 5 while 4d4 has mean deviation 5732 . In general, 2dn has mean deviation (n2 − 1) / 3n , but it quickly gets a lot more complicated. Roll can calculate the average and spread of a roll. Future versions might also compute the mean deviation.
The rules above can be used to calculate probabilities, mean and spread of any finite combination of dice (though some require complex enumeration of combinations). But what about open-ended rolls, i.e., rolls that allow unlimited rerolls of certain results? There is no way we can enumerate all combinations, so what do we do.
A simple solution it to limit the rerolls to some finite limit and, hence, get approximate answers (Roll, for example, does this). But it is, actually, fairly simple to calculate average and variance of rolls with unbounded rerolls.
Let us say that we have a roll that without rerolls has average M0 and you get a reroll with probability p and that when you reroll, the new roll is identical to the original (including the chance of further rerolls) and added on top of the original roll. This gives us a recurrence relation for the average M of the open-ended roll: M = M0 + p * M, which solves to M = M0/(1 − p) .
For an n-sided die has values x1 , . . . , xn and rerolls on xn , this yields M = (x1 + · · · + xn) / (n − 1) compared to the normal average M0 = (x1 + · · · + xn) / n.
The variance is more complicated[1]. If an n-sided die has values x1 , . . . , xn and rerolls on xn , the variance V is
Compared to the variance V0 of the same die without reroll:
As an example, let us take the dice-pool system from White Wolf 's “World of Darkness” game. In this system, you roll a number of d10s and count those that are 8 or more. Additionally, any 10 you roll adds another d10, which is also rerolled on a 10 and so on.
Without rerolls, the values are x1 , . . . , xn = 0, 0, 0, 0, 0, 0, 0, 1, 1, 1. So the average of one open-ended die is M = 3/9 = 1/3 . If you roll N dice, the average is N/3 . The variance of one WoD die is
As with normal dice, the variance of several open-ended dice add up, so the variance of N WoD dice is 8N 27 . Another example is an open-ended “normal” dn with rerolls on n. The average is M = (1 + · · · + n)/(n−1) = (n(n+1))/(2(n−1)) . The variance is
In calculating this, I have used the useful formulas
When talking about distribution of results (such as dice rolls), people often use the term bell curve to mean that the distribution looks somewhat like this:
I.e., reminiscent of a normal distribution. Strictly speaking, dice rolls have discrete probability distributions, i.e., the distributions map to bar diagrams rather than continuous curves, so you can't strictly speaking talk about bell curves. Additionally, mathematicians usually reserve the word for the normal (or Gauss) distribution, which is only one of may bell-shaped curves. A normal distribution is (roughly speaking) given by the formula p(x) = e−x2 .
Even so, you can say whether the bar diagram of a distribution resembles a bell curve, as does for example the classical 3d6 distribution:
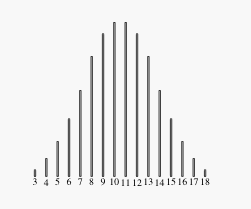
The main use of bell curves in RPGs is in generating attributes -- since “real world” attributes supposedly follow a normal distribution, people want this to be true in the game also. However, this is relevant only insofar as the in-game attributes translate linearly into real-world values. While this may be true for height and weight, etc., there is no indication that, for example intelligence in a game translates directly to IQ (which is defined to follow a normal distribution centered on 100). You can also argue that the same person performs the same task differently according to a distribution that resembles a normal distribution (when you can translate the quality of the result into a numeric measure), so you should use a bell-curved dice roll for action resolution. But again, this requires that the quality of results in the game translates linearly to some real-world scale, which is not always the case. For example, some games use a logaritmic scale on attributes or results, in which case using a normal distribution of attributes seems suspect. I don't say that using a bell curve is bad, but that it is sometimes unnecessary and sometimes misleading.
Many people use “bell curve” also when referring to non-symmetric distributions, such as the one you get for the sum of the three highest of 4 d6 (as used in d20 character generation), though this strictly speaking isn't a bell curve in mathematical terms. I will, like most gamers, use “bell curve” in the loose sense, but specify when bell-like distributions are non-symmetric.
In this section, we will look at some existing and new systems and discuss them in terms of the properties discussed in section 2. We will sometimes in this discussion calculate probabilities with the methods from section 3, but in other cases we will just relate observations about the probability distribution, which in most cases are obtained by using the Roll.
The simplest dice-roll mechanism is to use a single die. The result can be modified with ability, difficulty and circumstance in various ways.
There are many single-dice system, but the best known is the d20 system that originated in D&D. Here, a d20 is rolled, ability is added and a threshold determined by difficulty must be exceeded. Some opposed actions are handled by a contest of who gets the highest modified roll, while other opposed actions are treated by using properties of the opponent (such as armour class) to determine a fixed (i.e., non-random) difficulty rating. If the unmodified die shows 18-20, there is a chance of critical success: If a second roll indicates a successful action, the action is critically successful. As far as I recall, there is no mechanism for critical failures in the standard mechanics. Diminishing returns are handled by increasing costs of level increases.
Another single-die system is HârnMaster, where you roll a d100 and must roll under your skill (rounded to nearest 5) to succeed. If the die-roll divides evenly by 5, the success or failure is critical, so there is a total of four degrees of success/failure. The effective skill may be reduced by circumstance such as wounds and fatigue, but difficulty does not directly modify the roll. In opposed actions, both parties roll to determine degree of success and the highest degree wins. Ties in degree of success normally indicate a stalemate to be resolved in later rounds. Diminishing returns are handled by letting increase of skills be determined by dice rolls that are increasingly difficult to succeed (you must roll over the current ability on a d100 to increase it).
Talislanta (4th edition) uses a d20 to which you add ability and subtract difficulty. An “Action Table” is used to convert the value of the modified roll to one of five degrees of success/failure. Opposed rolls use the opponent's ability as a negative modifier to the active players roll. Diminishing returns is handled by increasing cost of skill increases.
So, even with the same basic dice-roll mechanism (roll a single die), these systems are quite different due to differences in how difficulty and circumstance modify the rolls, how opposed actions are handled, how degree of success is determined and how diminishing returns are achieved.
If we remove the trimmings, we have one system where you roll a die, add your ability and compare to a threshold. In the other, you roll a die and compare directly to your skill. Though these look different, they behave the same way (if the threshold in the first method is fixed): Increased ability will linearly increase the probability of success (until it is 1). Modifiers applied to the roll or threshold will also linearly increase or decrease the success probability. Such linear modification of probability is the basic property shared by nearly all single-dice systems.
I will pass no judgement about which of the above systems is best (and, indeed, this will depend on what you want to achieve), just note a few observations:
A variant of the above is adding up a few dice instead of a single die, but otherwise use the result as above (i.e., adding it to the ability, require it to be less than the ability, etc.).
An example is Stefan O'Sullivan's Fudge system that to the ability number adds four “Fudge dice” that each have the values −1, 0 and 1 (so a single Fudge die is equivalent to d3 − 2). This gives values from −4 to 4 added to the ability, which is then compared to the difficulty. The roll has a bell-like distribution centered on 0. Centering rolls on 0 has the advantage that ability numbers and difficulty numbers can use the same scale, so you can use the opponent's ability directly as difficulty without adding or subtracting a base value.
Another way of getting zero-centered rolls is the dn − dn method: Two dice of different colours (or otherwise distinguishable) are rolled, and the die with the “bad” colour is subtracted from the die with the “good” colour. The distribution is triangular and equivalent to dn + dn shifted down n + 1 places (i.e., to 2dn − n − 1). Another way of getting the same distribution is, again, to roll a good die and a bad die, but instead of subtracting the bad from the good, you select the die with the smallest number showing and let it be negative if it is on the bad die and positive if it on the good die (ties count as 0). For example, if the good die shows 6 and the bad die shows 4, the result is -4. This way, you replace a subtraction by a comparison, which many find faster. It takes a bit more explanation, though.
Another method equivalent to dn − dn is to have both sides in a conflict add a dn to their abilities. For unopposed actions, the GM acts opponent an adds the dn to a difficulty number. This allows the GM to hide the exact difficulty of an action (or ability of an NPC) from the players by rolling the opposing die secretly. It also means that the players get to roll whenever they are involved in an action, which keeps them active.
In general, having one side roll dn and the other roll dm is equivalent to letting the first side roll dn − dm or dn + dm − (m + 1). So there is no basic difference between having both sides roll and only one side roll, and the only difference between dn − dm and dn + dm is the constant m + 1.
The advantage of dn − dn (or equivalent) over Fudge dice is that you don't need special dice, but you do need players and GMs to be in agreement of which dice are good and bad before they are rolled. If you use dn + dn − (n + 1), you don't need this agreement, but you need one more arithmetic operation.
Since zero-centered dice-rolls (by definition) always have average 0, you can fairly easily take different degrees of randomness into account. For example, with dn − dn, you can use different n for different tasks: If the task has a low degree of variability, use d4s, if it has average variability, use d8s and if it has high variability, use d12s or even d20s. With Fudge dice, you can use three, four or five Fudge dice in a roll depending on how variable you want the result to be.
All of the above have non-flat distributions (and if more than two dice are involved, the distribution will be a bell curve), so adding a constant modifier will not increase the probability of success by a proportional percentage (as it does in single-dice systems). Some people dislike this by saying that the same modifier benefits some people more than others, but you can argue that this is the case for single-die systems too (if you, for example, look at the relative increase in success chance).
Another variant is to roll a small, fixed number of dice, but instead of adding them and comparing the sum to the ability, you compare each die value to the ability and count the number of dice that are lower. You can directly translate this number into a degree of success. If three or more dice are rolled, the degree of success will have an asymmetric bell-like distribution which is skewed towards low or high results depending on whether the ability is lower or higher than the mean value of a die. This mechanism limits the effective range of abilities to the range of a single die, but for games that operate with low granularity of abilities, this won't be a problem. And a d20 should accomodate enough ability levels to satisfy most.
Many games use a system where the ability of the character is translated into a number of dice that are rolled to determine success. In some of these systems, the dice are added to a single value, in others each die is independently compared to a threshold and the number of dice that meet or exceed this threshold are counted. Modifiers usually modify either the number of dice rolled, the required sum or count, the threshold towards which the dice are compared or even combinations of these.
Some examples:
Since the results of each die (which may be the straight value of the die or reduced to a smaller range of values, e.g., 0 or 1) are added, the average result increases linearly with ability, as does the variance. This has the effect that characters with higher ability have a larger spread in performance than do novice characters (although only in an absolute sense -- the spread divided by the average result decreases). If the results of action rolls translate to real-world figures, this may seem counter-intuitive, but since such translations rarely exist, it is largely a matter of taste whether this is good or bad.
If each increase in ability adds a die to the pool, you will quickly have to roll a very large number of dice unless the range of ability is limited. White Wolf 's systems limit attributes to a range of 1-5 and skills to a range of 0-5, so no more than 10 dice need to be rolled, and that only rarely. West End Games' d6 system (in some versions) has levels between adding a full die, which is another way to limit the number of dice rolled: You go from d6 to d6+1 to d6+2 to 2d6 and so on. Nevertheless, dice pools are usually used in games where there is no need for very fine-grained differences in ability.
The above-mentioned dice-pools are linear in the sense that adding more dice gives a linear increase in the average result. There are also games that use nonlinear dice-pools of various kinds.
One of the more complicated examples is from “Godlike” by Hobgoblynn Press. Here, you roll a number of d10 equal to attribute + skill, like in many other dice pool systems, but how you determine your result is quite different: You search for sets (pairs, triples, etc.) of identical dice-values and select one such set. The value on the dice determines how well you succeed and the number of dice in the set (called the width of the set) how quickly you do so.
If we ignore the width (and the optional “hard” and “wiggle” dice) and only look at the value of highest-valued set in a roll, we can see that the higher the value, the more likely it is. The reason is that the probability if getting a pair (or more) of a value doesn't depend on the value. All pairs are equally likely, but since you will choose the highest-valued pair if you get more than one, the final result is skewed towards higher values. If the number of dice is low, the skew is fairly small (as the chance of getting two or more sets is small), but at eight dice, a result of 10 is nearly seven times as likely as a result of 1. The chance of getting no sets (i.e., all different values) is initially quite high, but it drops to under 50% at five dice and is less than 2% at eight dice. The average result actually increases more than linearly with the number of dice (doubling the number of dice more than doubles the average), at least up to the maximum of 10 dice.
There are other nonlinear dice-pool systems. One of the simplest is to roll a number of dice equal to the ability and then pick the highest result, as is done in Dream Pod 9's “Silhouette”. Here is definitely a case of diminishing returns: With d10s, the average result starts at 5.5 and gets closer and closer to 10 when the number of dice increase, but will never reach it. The spread of the results decrease with the number of dice, so you can say that you reflect that more able persons are more consistent. However, the effect of the diminishing returns is maybe too great: Even a rank novice with ability 1 has 10% chance of getting the best possible result (10) and will have an average result that is more than half of what is maximally possible. Additionally, 10 (the maximum) is the most likely result already at ability 2.
To solve this, you can take the second-highest result of n dice (where n ≥ 2). There is still diminishing returns and decreasing spread, but much slower than before. In particular, the chance of getting a result of 10 increases much slower, so it isn't until 14 dice that it becomes the most likely result. The distributions (when n > 2) are bell curves skewed towards higher and higher values when n increases. Additionally, a character with skill 2 has only 1% chance of getting the best possible result.
Both the take-highest and take-second-highest method allow a low-skilled person a (low) probability of achieving the best possible result. Some like this possibility, but others want to put an upper limit on the results obtainable by low-skilled persons. A nonlinear dice pool that achieves this is that you (as always) roll a number of dice equal to you ability, but then count how many different results you get. This is bounded upwards by both the number of dice and the size of the dice used. There is also diminishing returns and decreasing spread. The main disadvantage is that it takes slightly longer to count the number of different values than to find the highest or second-highest of the values (though not by much). If you use n dM, the average number of different values is M( 1 - ( M-1/M )n ). For n d10, this simplifies 10(1 − 0.9n ).
Some dice-roll systems defy categorisation in the above classes. I will look at a few of these below.
The original “Sovereign Stone” game from Corsair Publishing (before it was assimilated by the d20 Borgs) used a fairly novel idea: Attributes and skills were given as dice types. So an attribute could range from d4 to d12 (with non-human attributes of d20 or d30 possible) and skills could range from 0 (nonexistant) through d4 to d12. When attempting a task, you would roll one die for your relevant attribute and another for your relevant skill and add the results. If the sum meets or exceeds the difficulty of the task, you succeed. The new “Serenity” RPG by Margaret Weis use a similar system, but starts from d2 instead of d4 and when you go past d12, you go to d12+d2, d12+d4, etc., instead of d20 and d30. In both systems, ratings over d12 are exceptional. An advantage of this system is that you (until you exceed a d12 rating) only do one addition to make a roll that takes attribute and skill into account, where adding skill and attribute to a die roll requires two additions. Additionally, the numbers are likely to be smaller, which makes addition faster. The disadvantage is that you need to have all types of dice around, preferably at least two of each. Additionally, the range of dice gives only five (or six) different values for attributes in the unexceptional range. This is fine for many genres, but not for all. It gets a bit more interesting if we look at the average and spread of results as abilities increase. If you add a dm and a dn, the average is m+n/2 + 1 and the variance is m2+n2-2/12 . If m = n, the average is n + 1 and the variance n2-1/6. This makes the spread (which is the square root of the variance) increase slightly faster than linearly in the average, which means that more skilled persons have higher spread -- even relative to their average -- than persons of lower skill. The main visible effect is that even very able persons have a high chance of failing easy tasks.
This observation has made someone suggest that higher abilities should equate smaller dice and low rolls be better than high. Though this makes higher skilled persons more consistent and prevents them from getting the worst possible results, it gives novices a fairly high chance of getting the best achievable result (“snake eyes”), which may be a problem if you want to make sure extremely able characters will always beat fumbling amateurs.
A system similar to the Sovereign Stone / Serenity system is used in Sanguine Productions' games, such as “Ironclaw” and “Usagi Yojimbo”. Here, three dice are rolled: One for attribute, one for skill and one for career. Instead of adding the dice, each is compared against two dice the GM rolls for difficulty. If one of the player's dice is higher than the GM's highest, the player succeeds, if two are higher, the player gets an overwhelming success. If all are smaller than the GM's smallest die, the player gets an overwhelming failure (the remaining cases are normal failures). Like the Sovereign Stone / Serenity system, you get increased spread of results with higher abilities. Also, since difficulties are rolled rather than being constants, high difficulties can sometimes be quite easily overcome (if the GM rolls low). All in all, this makes results quite unpredictable, with experts sometimes failing at simple tasks and novices sometimes succeeding at complex tasks. This will fit some genres, but not all.
The usual way of getting bell curves is by adding several dice (or counting successes, which is more or less the same), but you can do it also by comparing dice. A simple method is to roll three dice (e.g., d20s) and throw away the largest and smallest result, i.e., pick the median (middle) result. The advantage is that it requires no addition, so it is slighly faster than, say, adding 3d6. We will use the abbreviation “mid 3dn” for the median of three dn. We can calculate the probability of getting a result of x with mid 3dn by the following observation: The median is x either if either two or three dice come up as x, or one dice is less than x, one is equal to x and one is higher than x. The probability of all three coming up as x is 1/n3 . The chance that exactly two come up as x is 3 × 1/n2 × (n − 1)/n (the 3 comes from the three places the non-x die can be). The chance that there is one less than x, one equal to x and one greater than x is 6 × (x − 1)/n × 1/n × (n − x)/n (the 6 comes from the 6 ways of ordering the three dice). We can add this up to:
| 1/n3 + 3 × 1/n2 × (n − 1)/n + 6 × (x − 1)/n × 1/n × (n − x)/n | |
| = | { 1 + 3(n − 1) + 6(x − 1)(n − x) } / n3 |
| = | { 3n − 2 + 6(x − 1)(n − x) } / n3 |
| = | { -6x2 + 6(n + 1)x − (3n + 2) } / n3 |
For example, the chance of getting 7 on mid 3d10 is { 3 × 10 − 2 + 6(7 − 1)(10 − 7) } / 103 = 136/1000.
Since the curve is a parabola, it is arguable whether it can be called a bell-curve (it lacks the flattening at the ends), but it is a better approximation than 2dN. You can get closer to a “real” bell curve by taking the median of 5 dice instead of 3. This has the formula
For a given range of values, the curve obtained by taking the median of three dice is somewhat flatter than what you get by adding three dice, while the one you get by taking the median of five dice is slightly steeper than that of adding three dice. For example, all of the dice rolls below have ranges from 1 to 10 and averages of 5.5:
| Roll | Spread |
| mid 5d10 | 1.91 |
| 3d4-2 | 1.94 |
| mid 3d10 | 2.25 |
| d10 | 2.87 |
The value of the median roll is typically used in the same way as the value of a single die or the sum of a few dice (as described in sections 4.1 and 4.2).
If the value of the median roll is compared to ability (i.e., you must roll under your ability), the method is a special case of the method described at the end of section 4.2, except that you don't distinguish degrees of success and failure: If at least half of the individual dice meet the target, it is a success, otherwise a failure.
A variant is to combine median rolls with the idea of letting abilities equal dice types. So you would roll one dice for your attribute and another for your skill, but what about the third? You can add a third trait (like the career in “Ironclaw”), you can let the third die always be the same (e.g., always a d10), or you can duplicate the skill die, so you roll two dice for your skill and one for your attribute. This makes skills more significant than attributes and limits the maximum result to the level of the skill. Regardless, you still have the effect of spread increasing with ability that you get when the dice-sizes increase with ability.
If you want to handle powers of vastly different scales in the same game, some mechanisms break down or become unmanageable. For example, if the number of dice rolled is equal to your ability, what do you do if the ability is a thousand times higher than human average? And if you compare a roll against ability, all abilities higher than what the dice can show are effectively equal.
The first thing to do is consider how in-game values translate to real-world values. If this translation is linear (e.g., each extra point of strength allows you to lift 10kg more), you get very large in-game numbers. If you, instead, use a logarithmic scale (e.g., every point of strength doubles the weight you can lift), you can have very large differences in real-world numbers with modest differences in in-game numbers.
Doubling the real-world values for every step is rather coarse-grained, so you may want a few steps betwen each doubling. A scale that has been used by several designers is to double for every three steps. This means that every increase multiplies the real-world value by the cube root of two (1.25992). This is sufficiently close to 1.25 that you can say that every step increases the real-world value by 25%. Another thing that makes this scale easy to use is that 10 steps multiply the real-world value by almost exactly 10 (10.0794, to be more precise), so you can say that 10 steps in a factor of 10 with no practical loss of precision. Some adjust the scale slightly, so 10 steps is exactly a factor of 10, which makes three steps slightly less than a doubling, but close enough for practical use. The decibel scale for sound works this way: Every increase of 10dB multiplies the energy of the sound by 10.
Even so, you may get numbers that are too large to be practically manageable (e.g., in dice pools or when you use dice-types to represent abilities), so you can add a scaling mechanism that say that for every increase of N in ability, you are at one higher scale.
When resolving an action between two entities, you reduce (or increase) both scales such that the weakest of the two entities is at scale 0. For example, if N = 10 (i.e., every increase of 10 increases scale by 1) and a struggle between one entity of ability 56 and another of ability 64, you reduce it to a battle between abilities of 6 and 14. You can add an additional rule that if the difference in scale is more than, say, 2, then you don't roll: The higher scale automatically wins.
Issaries' “Heroquest” game integrates a scale system directly: A unit of scale (or “Mastery”) is a difference of 20, and you denote an ability as a number between 1 and 20 plus a number of Masteries. You must roll under your ability number on a d20 to succeed, but each Mastery increases the degree of success by one (or reduces that of the opponent by one).
One thing to note, though, is that not all abilities have real-world measures: How do you measure beauty numerically? Or agility, leadership or intelligence? The latter has a numeric measure (IQ), but this is an artificial construction, defined to average to 100 and be normally distributed around this, so saying that someone with an IQ of 160 is twice as intelligent as one with IQ 80 is silly. When games assign numbers to such unquantifiable properties and abilities, these numbers are as much a construction as IQ numbers, and can really only be used to determine how well the characters measure relatively to each other (or to arbitrary GM-decided difficulty numbers).
Here I will briefly look at other ways of bringing randomness into games.
Next to dice, cards seem to be the most common randomizer in RPGs. Some games (like R. Talsorian's “Castle Falkenstein”) use standard playing cards, others (like TSR's “Saga” system) invent their own.
Draws of cards from the same deck are, unlike die rolls, not independent events, so analysing probabilities becomes more complex. Some argue that this makes cards superior -- “luck” would tend to even out, as you will get all numbers equally often if all cards in a deck are drawn before it is reshuffled. But this assumes that all draws are equally important, which I find questionable.
The main advantages of using cards over dice are:
Not all of these will be relevant to all games, though, and some may dislike having the players choose their “luck” from a hand of cards, as it brings meta-game decisions into the game world. Additionally, you can have players doing unimportant tasks simply to get rid of bad cards in a safe way.
Spinners are really just dice of a different shape -- you get (usually) equal probabilities of a finite number of outcomes. The main advantage of spinners is that you can make them in sizes (number of outcomes) that you don't find on dice, such as 7 or 11 or unequal probabilities of different results, (depending on the size of the corresponding pie slices). Additionally, spinners can be cheaper to make than specialized dice, such as Fudge dice.
While this strictly speaking isn't random, it is unpredictable enough that it can be used as a randomizer. Its sole advantage is that it doesn't require any equipment or playing surface, which makes it popular in live role-playing.
There are really only three outcomes: Win, lose and draw, each of which have equal probabilities (assuming random or unpredictable choices), but you can add in special cases, such as special types of characters winning draws on certain gestures. For example, warriors could win when both hands are “rock”, magicians when both are “paper” and thieves when both are “scissors”. Also, it only works with two players, as you otherwise can get circular results (A beats B, who beats C who beats A), which can be hard to interpret.
There are generalisations of rock-paper-scissors to five or seven different values that avoid cycles with three or four players, but these tend to be harder to remember.
On the rpg-create mailing list there are often requests for dice-roll mechanisms with certain specific properties, usually regarding the probability distribution. For example, one poster asked for a dice-roll mechanism that would allow the GM to change the variance while retaining the same range and average.
More specifically, he wanted a family of similar dice-roll mechanisms that all share range and average but which have different variance, so the GM can choose higher variance for more chaotic events and lower spreads for less chaotic events.
There are many ways to achieve this. For example, the median-of-three-dice metod decribed in section 4.5.2 can be generalised to taking the median of N dice, where N is any odd number. Increasing N will decrease the variance, but only very slowly, so you will need a very large number of dice to get a small variance.
An alternative is to look at mdn + k. As described in section 3.3, the average of m dn + k is m × (n + 1)/2 + k and the variance is V = m × (n2 − 1)/12 . The range is, obviously, from I = m + k to S = m × n + k. Note that the average is exactly midway between the two extremes (since the distribution is symmetric), so we need only look at the range and variance.
To get a family of mdn + k with identical range, we need to find sets of m, n and k that give the same values for
| I | = | m + k |
| S | = | m × n + k |
while allowing different values of V = m × (n2 − 1)/12.
We can derive:
| m | = | (S − I) / (n − 1) |
| k | = | I − m |
Now, since m must be an integer, we want n − 1 to divide evenly into S − I . 12 has many divisors, so we could try with S − I = 12, which gives:
| m | = | 12 / (n − 1) |
| k | = | I − m |
| V | = | 12/(n − 1) × (n2-1)/12 = n + 1 |
Since we want a range of values, n must be at least two (otherwise we don't get a range of results). For different values of n, we get:
| n | m | V |
| 2 | 12 | 3 |
| 3 | 6 | 4 |
| 4 | 4 | 5 |
| 5 | 3 | 6 |
| 7 | 2 | 8 |
| 13 | 1 | 14 |
So we can get six different variances for the same range of values. Note that (through choice of I ) we can choose where to place the range of values. We can, for example, choose 1 · · · 13 or −6 · · · 6. The latter gives us the following rolls:
| Roll | V | spread (SQRT(V)) |
| 12d2 − 18 | 3 | 1.73 |
| 6d3 − 12 | 4 | 2 |
| 4d4 − 10 | 5 | 2.24 |
| 3d5 − 9 | 6 | 2.45 |
| 2d7 − 8 | 8 | 2.83 |
| 1d13 − 7 | 14 | 3.74 |
The method does require use of non-standard dice like d2, d3, d5, d7 and d13, though.
For a table-top RPG, we would prefer the standard polygonal dice: d4, d6, d8, d10, d12 and possibly d20. Since S − I must divide evenly by n − 1, we want a number that divides evely by 3, 5, 7, 9, 11 and possibly 19. The smallest number that divides evenly by all of these is 65835, which would require adding up a ridiculous number of dice. Forgetting about 9, 11 and 19 gives us 105 which is still a tad high, and any lower gives us only two options, which sort of defeats the purpose. In conclusion, we can't really make the idea work with standard dice.
Here, I will discuss a few personal preferences and pet peeves. Unlike the above, where I have (mostly) tried to be neutral and objective, rampant subjectivity will abound. So you are warned.
I don't like rerolls. They take extra time that you can't decrease much by experience -- the physical action of rolling again can't really be sped up. This is in contrast to time used for calculations based on a single roll, such as adding up the dice or counting successes, which you can decrease almost arbitrarily with training.
Additionally, repeated rerolls remove upper limits on rolls -- anyone can conceivably achieve fantastical results, just not very often. It can spoil any game if a street kid kills the dragon that menaces the town by throwing a stone at it, just like it will spoil the game if that same brat downs a high-level PC. Also, the absence of an upper limit will make players insist on rolling even when they are hugely overpowered, on the off chance that they will reroll a dozen times. Sure, the GM can forbid such silliness, but then why have rerolls at all?
Some argue that heroic fiction abounds with cases where the hero wins over a vastly more powerful foe (such as Bard the bowman in “The Hobbit” killing Smaug with a single arrow), but this is usually because of outrageous skill rather than outrageous luck.
A third problem I see with rerolls is that they make the probability distribution uneven: You can get holes in the distribution (i.e., impossible results) or places where the probability drops sharply but then stays nearly constant for a while.
Many games, especially Indie or homebrew, feature “innovative” dice-roll mechanisms that seem to be different just for the sake of being new. Like haut couture fashion, these are often overly complex and don't seem to add anything other than change and strangeness to what they replace. Such can serve one legitimate purpose -- it can get your game noticed where yet another d20 game won't. But it is better to combine innovation with purpose -- make the new system do something that can't (as easily) be achieved with existing systems, without sacrificing the good properties of tried-and-tested methods.
Though I may get flak for this, I find Godlike's mechanism (as described in section 4.4) to be an example of haut couture dice mechanims -- it is quite complex, the probabilities are weird and it doesn't seem to do much that you couldn't achieve by simpler means.
I haven't covered all resolution mechanisms that use dice -- partly because of space, partly because of defective memory and just not knowing them all. And I'm sure many new dice-roll mechanisms will be invented, some to be deservedly forgotten again and others to be copied over and over with minor variations.
Whether you plan to use an existing method or invent your own, I hope this paper has given you something to think about when doing so. And stay tuned -- I will at uneven intervals release new versions of this document to the public (compare the dates to see if you have the newest version).